Max Maths, Year 5, Try it, Reflective and rotational symmetry in regular polygons (1)

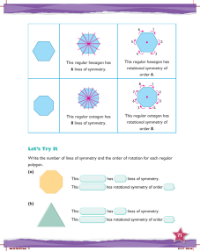
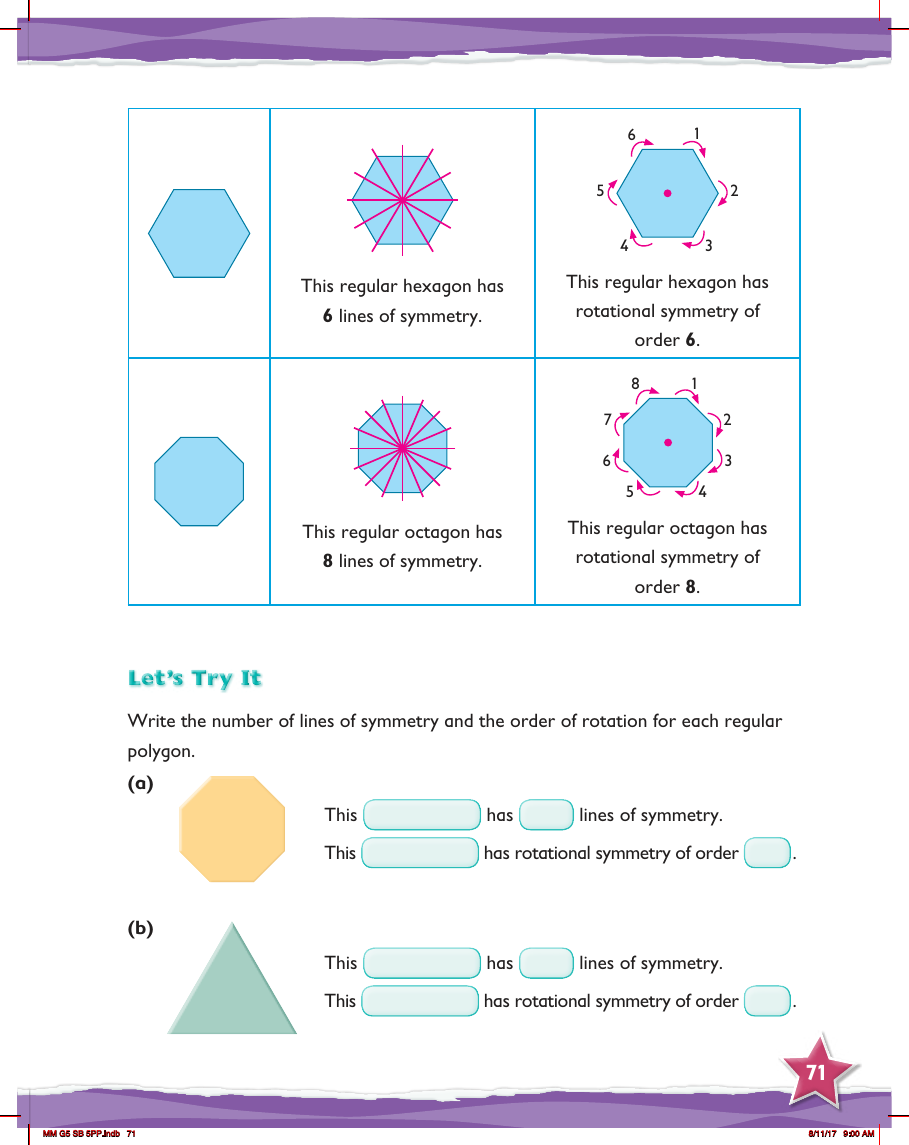
In a mathematics lesson for Year 5, students explore the concepts of reflective and rotational symmetry within regular polygons. A regular hexagon is used as an example to illustrate that it possesses 6 lines of symmetry, meaning there are six different ways it can be folded along a line so that both halves match perfectly. Additionally, the same hexagon is shown to have rotational symmetry of order 6, which means it can be rotated around its centre point in increments that correspond to one-sixth of a full turn, and it will still look the same each time.

Similarly, the lesson moves on to a regular octagon, which is demonstrated to have 8 lines of symmetry. These lines indicate the number of ways the octagon can be folded over itself to produce mirrored halves. Furthermore, the octagon is described as having rotational symmetry of order 8, signifying that the shape can be rotated to eight different positions around its centre, each at an angle equivalent to one-eighth of a full rotation, and it will maintain its appearance. Students are then encouraged to apply this knowledge by writing down the number of lines of symmetry and the order of rotational symmetry for additional regular polygons presented in the exercise.