Algebra - Find pairs of values (1) - Planning

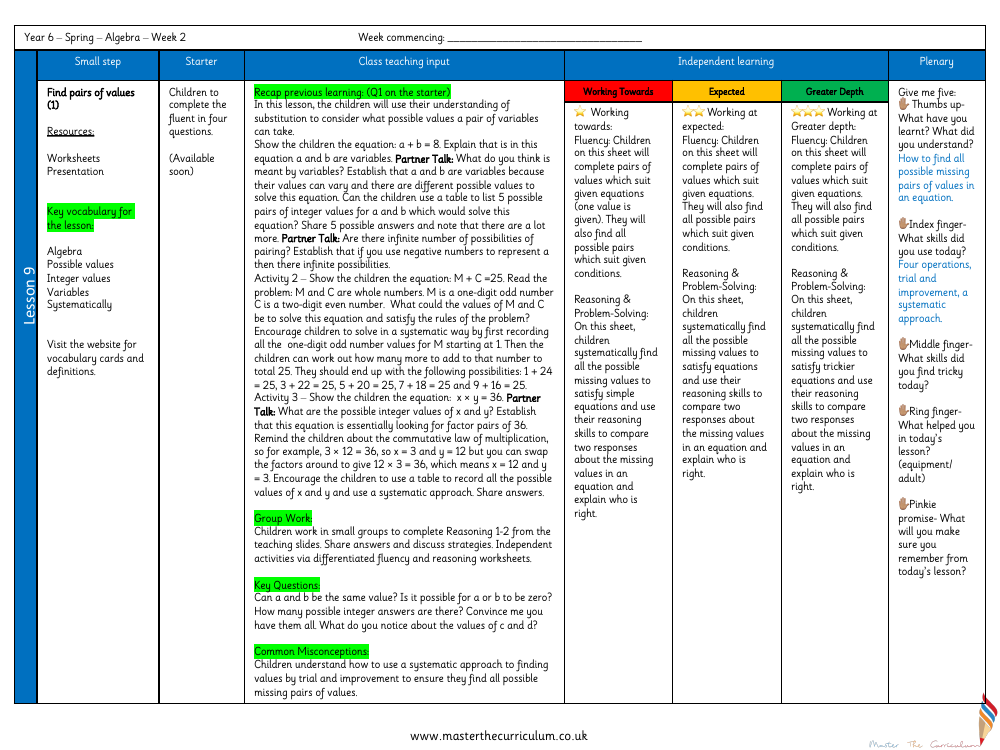
In the second week of the Spring term, Year 6 students delve into algebra with a focus on finding pairs of values that satisfy given equations. The lesson begins with a starter that recaps substitution, setting the stage for exploring variable pairs. Using the example equation a + b = 8, students are asked to list five possible integer pairs for the variables a and b that would solve the equation. This exercise introduces the concept of variables as quantities that can vary, and encourages students to consider whether there are infinite possibilities for such pairings, especially when negative numbers are introduced. The class then moves on to a more complex problem, M + C = 25, where M is a one-digit odd number and C is a two-digit even number. Students are guided to approach this problem systematically, starting with the smallest odd number for M and finding the corresponding C that adds up to 25, leading to a set of possible solutions.

The lesson continues with an equation involving multiplication, x × y = 36, where students must find factor pairs of 36. This activity reinforces the commutative law of multiplication and prompts students to systematically record all possible integer values for x and y. During group work, students tackle reasoning tasks from the teaching slides, sharing their answers and discussing strategies. The lesson's key questions challenge students to consider the uniqueness of solutions and the possibility of zero as a value. They are encouraged to use a systematic approach to ensure they identify all possible pairs of values. The lesson concludes with a reflective 'Give me five' exercise where students consider what they've learned, the skills they've used, such as the four operations and trial and improvement, and what they found challenging. Differentiated worksheets for fluency, reasoning, and problem-solving cater to varying levels of understanding, from working towards fluency to achieving greater depth in algebraic problem-solving.