Multiplication and Division (2) - Divide 2-digits by 1-digit (remainder) - Planning

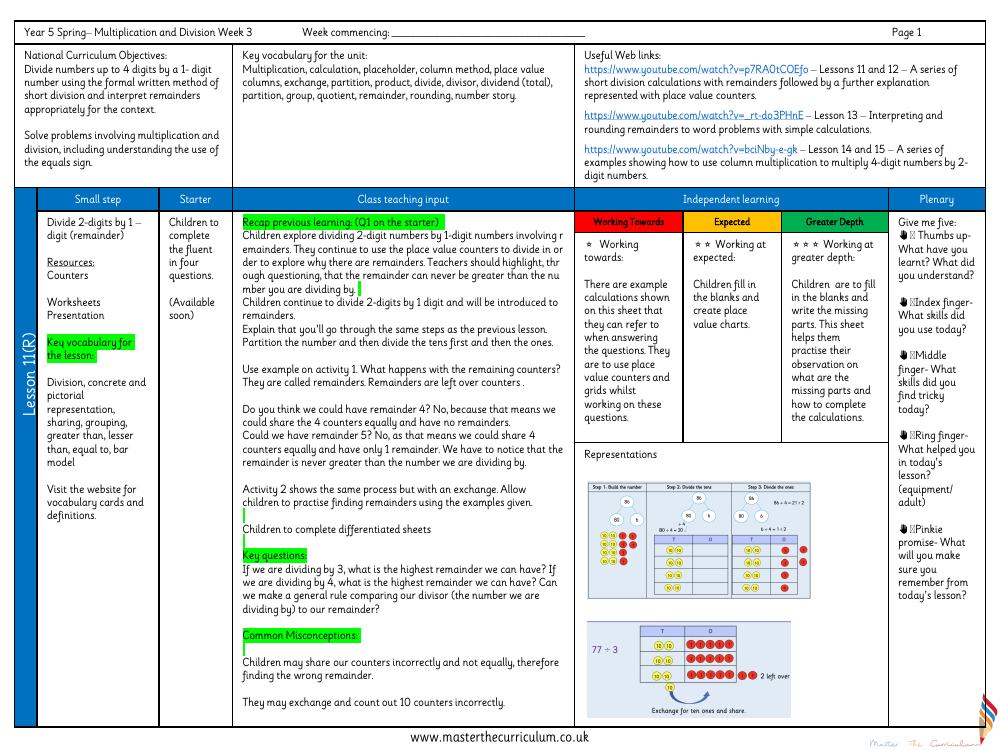
In this Year 5 lesson, students delve into the world of division, specifically focusing on dividing 2-digit numbers by 1-digit numbers and understanding remainders. The National Curriculum objectives are clear: students must learn to use the formal written method of short division and interpret remainders in a way that suits the context of the problem. The lesson incorporates a variety of key vocabulary terms such as division, quotient, and remainder, which are integral to grasping the concept. Using concrete and pictorial representations, such as counters and bar models, the lesson aims to solidify the students' understanding of division and the significance of remainders. The lesson begins with a recap of previous learning, ensuring students remember that a remainder can never exceed the divisor, and progresses through partitioning numbers to divide tens and ones, leading to independent practice with differentiated worksheets.

The structure of the lesson is designed to cater to different levels of understanding, from working towards the expected level to achieving greater depth. Students are encouraged to reflect on their learning through a "Give me five" activity, where they consider what they have learned, the skills they have used and found tricky, what supported their learning, and what they need to remember moving forward. To assist with varying abilities, example calculations and resources such as place value counters and grids are provided. As students advance, they are challenged to fill in blanks and create place value charts, enhancing their ability to observe and complete calculations independently. The lesson is rounded off with a plenary that addresses common misconceptions, such as incorrect sharing of counters or errors in exchanging, ensuring that students leave with a robust understanding of division with remainders.